Introduction
In the realm of computer science and binary mathematics, a fascinating challenge is presented: Given an integer, can we find the next smallest and largest numbers that have the same number of 1 bit as the given number?
In this article, we will solve this problem using three distinct approaches: brute force, bit manipulation, and an arithmetic strategy. We will explore the logic and Python code behind each method, providing a comprehensive understanding of the problem-solving process.
Understanding the Problem
Before we dive into the solution, let’s break down the problem statement. Given an integer, we are tasked with finding two distinct integers that meet the following criteria:
- They have the same number of 1 bits (also known as “set bits”) as the given integer.
- The first number should be the smallest possible integer that meets the criteria.
- The second number should be the largest possible integer that meets the criteria.
Brute Force Approach
The Brute Force Approach is the easiest way to solve the given problem. Before moving to the Optimal Solution, let’s get a little intro with two Python Programs. These programs demonstrate the application of the Brute Force technique to determine the Next and Previous Numbers.
Brute Force Approach to Get the Next Number
The logic is quite straightforward. Examine the following steps:
- Calculate the count of ‘1’s in the provided positive integer and save it in a variable.
- Enter a while loop that continues as long as the condition is met.
- Increase the current number by one.
- Recalculate the count of ‘1’s in the updated current number.
- If the count of ‘1’s in the original number matches the count in the current number, the program will yield the current number as the output result.
Python Implementation
def countOnes(num):
count = 0
while num:
count += num & 1
num >>= 1
return count
def getNext(num):
countGivenNum = countOnes(num)
n = num
while True:
n += 1
if countOnes(n) == countGivenNum:
return n
if __name__ == "__main__":
num = int(input("Please Enter the Number: "))
nextNum = getNext(num)
print("Next Largest Number: ", nextNum)
Output
Please Enter the Number: 8888
Next Largest Number: 8899
Brute Force Approach to Get the Previous Number
The approach’s logic closely resembles the previous one, with the only difference being that in this instance, we will decrease the provided number by one during Step 3.
Python Implementation
def countOnes(num):
count = 0
while num:
count += num & 1
num >>= 1
return count
def getPrevious(num):
countGivenNum = countOnes(num)
n = num
while True:
n -= 1
if countOnes(n) == countGivenNum:
return n
if __name__ == "__main__":
num = int(input("Please Enter the Number: "))
prevNum = getPrevious(num)
print("Previous Largest Number: ", prevNum)
Output
Please Enter the Number: 8888
Previous Largest Number: 8884
Bit Manipulation Approach
Using bit manipulation, we can efficiently find the next smallest and largest numbers by changing the bits that maximize or minimize the value while maintaining the count of the set bits.
We will divide this discussion into two parts. The initial part will address obtaining the next number sharing the same count of 1 bits in its binary representation while the second part will focus on obtaining the previous number.
Bit Manipulation Approach to Get the Next Number
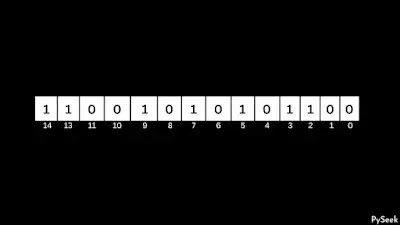
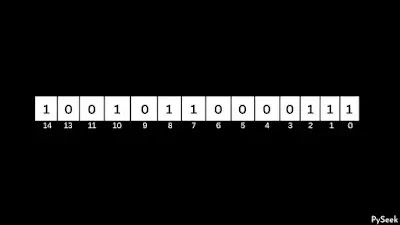
To understand the problem better, let’s consider the positive integer 12972 as an example. We want the next number with the same number of 1s.
 |
| Binary representation of the given number |
Consider a number ‘n’, along with the positions of two bits, denoted as ‘i’ and ‘j’. If we invert the bit at position ‘i’ from 1 to 0 and the bit at position j from 0 to 1, the number ‘n’ will decrease if ‘i > j’. Conversely, if ‘i < j’, the number ‘n’ will increase.
Keep in Mind
1. If we flip a bit from zero to one, we must flip another bit from one to zero.
2. If we do that, the number will be bigger if and only if the zero-to-one bit is to the left of the one-to-zero bit.
3. We want the next larger number, not unnecessarily bigger.
See the following steps:
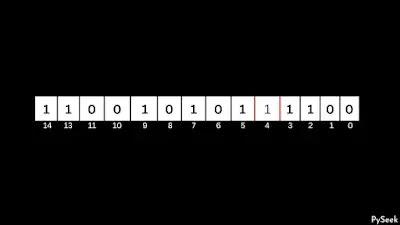
Step 1: Flip the rightmost non-trailing zero
In the above example, the rightmost trailing zeros are in the 0th and 1st position and the position of the rightmost non-trailing zero (zero followed by 1) is 4. We will call this position ‘p’.
Now we flip ‘p’ zero-to-one.
 |
| Flip the rightmost non-trailing zero |
Following this change, the size of ‘n’ has been increased. Our subsequent task involves reducing the size of ‘n’. Prior to that, we will count ‘count0’ (number of zeroes after ‘p’) and ‘count1’ (number of ones after ‘p’).
Now we get: “count0=2“, “count1=2“, “p=4“.
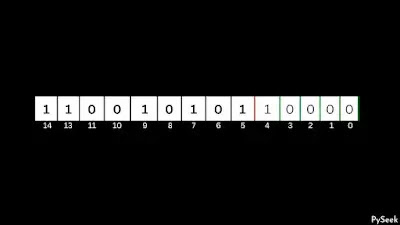
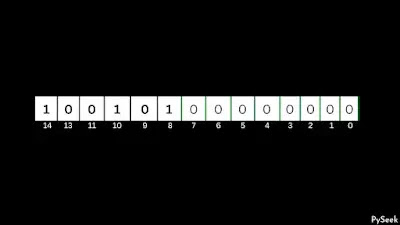
Step 2: Clear bits to the right of ‘p’
At this step, we will reset all the bits (set to zero) situated to the right of ‘p’.
 |
| Clear all the bits to the right of ‘p’ |
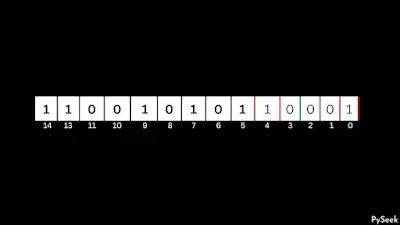
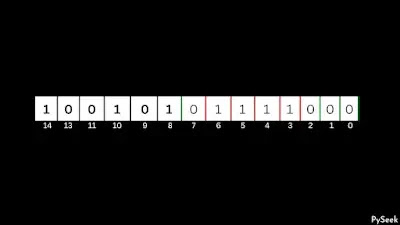
Step 3: Add ‘count1 – 1’ number of ones (1s) on the right side
In the final stage, we should insert a total of ‘count1-1’ occurrences of ones (1s) at the extreme right position. Consequently, we will get the subsequent larger number compared to the given value n, while preserving an equal count of 1s in its binary representation.
 |
| Add the ‘count-1’ number of ones to the extreme right position |
Python Implementation
def getNext(num):
c = num
count0 = 0
count1 = 0
# Computing count0: Number of zeros to the right of p
while (((c & 1) == 0) and (c != 0)):
count0 += 1
c >>= 1
# Computing count1: Number of ones to the right of p
while ((c & 1) == 1):
count1 += 1
c >>= 1
# If num == 11..1110...00, then there is no bigger
# number with the same number of 1s.
if count0 + count1 == 31 or count0 + count1 == 0:
return -1
# Position of rightmost non-trailing zero
p = count0 + count1
# Flip the rightmost non-trailing zero
num |= (1 << p)
# Clear all bits to the right of p
num &= ~((1 << p) - 1)
# Insert (count1-1) ones(1s) on the right
num |= (1 << (count1 - 1)) - 1
return num
if __name__ == "__main__":
num = int(input("Please Enter the Number: "))
nextNum = getNext(num)
print("Next Number: ", nextNum)
Output
Please Enter the Number: 12972
Next Number: 12977
Bit Manipulation Approach to Get Previous Number
In this scenario, the approach closely resembles the previous one, with a subtle distinction. Let’s consider a different number, 9607, as an example this time. Our objective is to determine the previous number that maintains the same count of 1s.
Consider the given number n, along with the positions of two bits, denoted as i and j. We perform a bit flip operation by changing the bit at position i from 1 to 0 and the bit at position j from 0 to 1. In this case, ‘i>j’.
See the following steps:
Step 1: Compute Initial Numbers
First, we need to compute ‘count1’ (number of trailing ‘1s’), ‘count0’ (size of the block of ‘0s’ just to the left of the trailing ‘1s’), and ‘p’ which is the rightmost non-trailing one (a ‘1’ followed by a ‘0’). We can get ‘p’ this way: “p = count0 + count1”.
 |
| The Binary representation of a positive integer number |
According to the above example, we get “count1 = 3”, “count0 = 4”, and “p = 7”.
Step 2: Clear all the bits through ‘p’
After this operation, the binary representation will look like the following:
 |
| Clear all the bits through ‘p’ |
Step 3: Add the ‘count1 + 1’ number of ones just after to the right of ‘p’
After this step, we will get our desired result.
 |
| Add (count+1) number of ones just after the ‘p’ |
This is the previous number of the given integer, sharing an equivalent count of ‘1’ bits.
Python Implementation
def getPrev(num):
c = num
count0 = 0
count1 = 0
# Computing count1: Number of ones to the right of p
while ((c & 1) == 1):
count1 += 1
c >>= 1
if c == 0:
return -1
# Computing count0: Number of zeros to the right of p
while (((c & 1) == 0) and (c != 0)):
count0 += 1
c >>= 1
# Position of rightmost non-trailing one
p = count0 + count1
# Clear all bits to the right of p
num &= ((~0) << (p + 1))
# Sequence of (coun1+1) ones
mask = (1 << (count1 + 1)) - 1
num |= mask << (count0 - 1)
return num
if __name__ == "__main__":
num = int(input("Please Enter the Number: "))
prevNum = getPrev(num)
print("Previous Number: ", prevNum)
Output
Please Enter the Number: 9607
Previous Number: 9592
Arithmetic Approach
In this section, we will solve the same challenge utilizing arithmetic techniques. Similar to the Bit Manipulation approach, we will develop two distinct programs here: one to determine the next number and another to find the previous number.
Arithmetic Method to Get the Next Number
Remember the steps we followed in the bit manipulation approach to get the bigger number. An overview of these steps is presented below:
Step 1: Set the rightmost non-trailing zero (or ‘p’) to 1.
Step 2: Clear all the bits to the right of the ‘p’.
Step 3: Add (‘count1-1’) number of ones (1s) at the extreme right position.
All the above steps can be performed using an alternative way.
A quick way to accomplish Step 1 and Step 2 involves converting trailing zeros to ones and subsequently incrementing the number by 1 (or adding 1 to the number).
Let’s grasp this concept by looking at the following example:
Assume, n=1010101100. We set trailing zeros to 1. Now, n=1010101111.
Next, we increment the number ‘n’ by 1 (‘n+1’). Now, n=1010110000.
We can execute these two steps using arithmetic methods in the following way:
n = n + (2^count0) – 1 # Sets trailing 0s to 1, giving us ‘p’ trailing 1s.
n = n + 1 # Flips first ‘p’ 1s to 0s, and puts a 1 at the position of ‘p’.
Now, we do the following operation to perform Step 3 arithmetically.
n = n + (2^(count1-1)) – 1) # Sets trailing (count1 – 1) zeros to ones (1s)
If we reduce the entire math, it would be like this,
nextNumber = n + ((2^count0) – 1) + 1 + (2^(count1-1)) – 1)
“nextNumber = n + (2^count0) + (2^(count1-1)) – 1″
Python Implementation
def getNext(num):
c = num
count0 = 0
count1 = 0
# Computing count0: Number of zeros to the right of p
while (((c & 1) == 0) and (c != 0)):
count0 += 1
c >>= 1
# Computing count1: Number of ones to the right of p
while ((c & 1) == 1):
count1 += 1
c >>= 1
# If num == 11..1110...00, then there is no bigger
# number with the same number of 1s.
if count0 + count1 == 31 or count0 + count1 == 0:
return -1
# Position of rightmost non-trailing zero
p = count0 + count1
return num + (1 << count0) + (1 << (count1 - 1)) - 1
if __name__ == "__main__":
num = int(input("Please Enter the Number: "))
nextNum = getNext(num)
print("Next Number: ", nextNum)
Output
Please Enter the Number: 684
Next Number: 689
Arithmetic Method to Get Previous Number
If you remember the steps we followed in the bit manipulation approach to get the previous number, we took ‘count1’ as the number of trailing ones, ‘count0’ as the size of the block of zeros just to the left of the trailing ones, and p=count0+count1. Here, we will also keep the scenario as it is.
Now if we summarize the steps from there, it would be as follows:
Step 1: Set the bit at position ‘p’ to 0.
Step 2: Clear all the bits to the right of ‘p’.
Step 3: Add the ‘count1+1’ number of ones just to the right of ‘p’.
All these steps can be performed arithmetically also.
Assume, n=1010100011. According to this example, count1=2, count0=3.
Clear trailing ones. Now ‘n’ is 1010100000
Arithmetically: n = n – (2^count1) – 1
Flip trailing zeros. Now ‘n’ is 1010011111
Arithmetically: n = n – 1
Flip last ‘count0 – 1’ 1s. Now ‘n’ is 1010011100
Arithmetically: n = n – (2^(count0 – 1) – 1)
Simplifying the entire mathematical process yields a form similar to the one presented below:
prevNumber = n – ((2^count1) – 1) – 1 – (2^(count0 – 1) – 1)
“prevNumber = n – (2^count1) – (2^(count0 – 1)) + 1“
Python Implementation
def getPrev(num):
c = num
count0 = 0
count1 = 0
# Computing count1: Number of ones to the right of p
while ((c & 1) == 1):
count1 += 1
c >>= 1
if c == 0:
return -1
# Computing count0: Number of zeros to the right of p
while (((c & 1) == 0) and (c != 0)):
count0 += 1
c >>= 1
# Position of rightmost non-trailing one
p = count0 + count1
return num - (1 << count1) - (1 << ( count0 - 1)) + 1
if __name__ == "__main__":
num = int(input("Please Enter the Number: "))
prevNum = getPrev(num)
print("Previous Number: ", prevNum)
Output
Please Enter the Number: 675
Previous Number: 668
Reference
Cracking the Coding Interview (Bit Manipulation, Problem #5.4) – Book by Gayle Laakmann McDowell
Summary
In this article, we explored three diverse approaches to solving the challenge of finding the next smallest and largest numbers with the same number of 1 bits as a given integer. The brute force method provides a basic solution, while the bit manipulation and arithmetic approaches offer more optimized and elegant solutions. Each approach highlights the power of understanding bitwise operations and mathematical patterns to efficiently solve binary-related problems.
By presenting these techniques and their corresponding Python implementations, this article equips you with the tools to tackle similar problems with confidence and creativity.
